Polymer dynamics
Our current theoretical understanding of entangled polymer chain dynamics is based on the reptation model. First proposed by Doi and Edwards, and further expanded by de Gennes, the reptation model assumes that a polymer chain is confined by the surrounding matrix and is therefore forced to move inside an imaginary tube defined by the transient network of entangled neighboring chains. Intuitively this motion resembles that of a snake or worm. The reptation model predicts five dynamical regimes for segment diffusion, summarized in the figure below. These regimes are as follows: (0) sub-segmental processes (“glassy dynamics”) at very short times (microseconds), (I) small motion subject only to chain connectivity, (II) “local reptation”: short-distance motion within the constraints imposed by the surrounding chains (“tube”), (III) “reptation”: diffusive motion along the curvilinear tube over distances larger than the polymer size, and (IV) free diffusion.
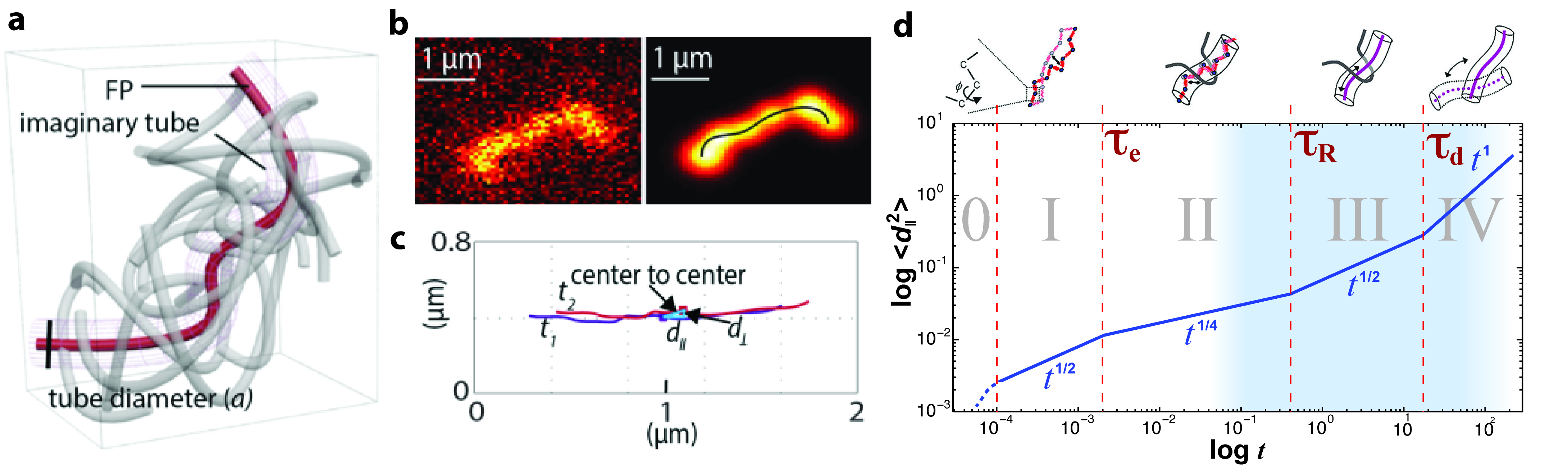
While reptation theory has proven to be a powerful tool, there are significant discrepancies between its predictions and the experimental results. These differences mainly arise because the model neglects the presence of cooperative network interactions – differences in segment diffusion due to tube diameter variations and different local friction between monomer units and the matrix are ignored. While there is substantial interest in developing improved models, one of the limitations has been the difficulty in acquiring experimental data that can truly resolve the heterogeneity of polymer dynamics, preferably by avoiding ensemble averaging entirely and observing just a single chain.
In this project we aim to directly visualize the reptation motion by tracking the motion of individual fluorescently labeled polymer chains in a matrix of unlabelled polymer molecules using 3D SOFI (see Technologies).
For more information:
- Keshavarz M., et al. (2016) Nanoscale Study of Polymer Dynamics, ACS Nano, 10(1), pages 1434–1441 (article can be found here)